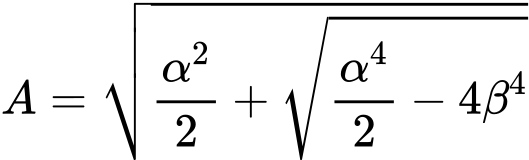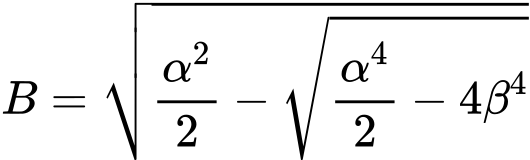Geometrická (Eulerova) metoda
Prostředí kolem mikropiloty je v programu modelováno modulem reakce podloží Ep (winklerovskou konstantou k), která je zadávána uživatelem v rámu "Posouzení průřezu". Model konstrukce je znázorněn na obrázku.
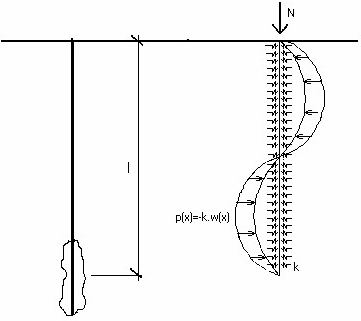 Model konstrukce
Model konstrukce
U tlačené mikropiloty je předpokládán vznik proměnného počtu polovln v závislosti na geometrii a tuhosti konstrukce resp. prostředí. Řešení tohoto případu vychází z rovnice ohybu přímého prutu.
![]()
Po úpravách lze ohybovou rovnici vyjádřit ve tvaru:
| |
kde: | |
| |
| |
| |
|
Pro výpočet integračních konstant C1-C4 se použije čtyř okrajových podmínek, které vyjadřují způsob uložení konců.
Velikost kritické síly Ncr lze spočítat pomocí obecného vztahu známého z teorie pružnosti (viz literaturu [1]):
![]()
kde: | Ei | - | modul pružnosti ideálního průřezu |
Ii | - | moment setrvačnosti ideálního průřezu | |
lp | - | efektivní délka mikropiloty (volná délka mikropiloty + 1/2 délky kořene) | |
Er | - | ||
n | - | počet půlvln ohybové čáry po délce mikropiloty |
Kritická síla Ncr se hledá jako minimum funkce (1). Toho je dosaženo pro délku půlvlny
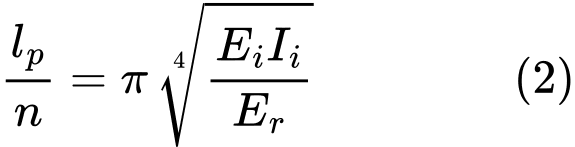
Z rovnice (2) vyplývá vztah pro počet půlvln n:
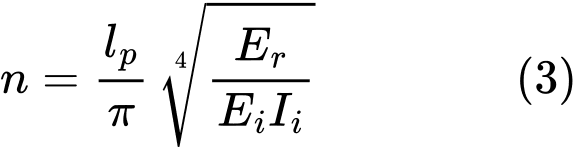
Pokud je mikropilota umístěna zčásti nad zeminou (vysazení), stanoví se redukované hodnoty n a Er s ohledem na délku mikropiloty nad zeminou:
![]()
![]()
kde: | lv | - | délka mikropiloty nad terénem |
Pro uložení mikropiloty kloub-kloub se kritická síla Ncr určí ze vztahu:
![]()
Pro uložení mikropiloty kloub-vetknutí se kritická síla Ncr určí ze vztahu:
![]()
Literatura:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936